2.
Expressions, Variables & Constants
Written by Irina Galata
In this second chapter, you’re going to learn a few basics. You’ll learn how code works first. Then, you’ll start your adventure into Kotlin by learning some basics such as code comments, arithmetic operations, constants and variables. These are some of the fundamental building blocks of any language, and Kotlin is no different.
First of all, you’ll cover the basic workings of computers, because it really pays to have a grounding before you get into more complicated aspects of programming.
How a computer works
You may not believe it when you hear it, but a computer is not very smart on its own. The power of computers is all derived from how they’re programmed by people like you and me. If you want to successfully harness the power of a computer — and presumably you do, if you’re reading this book — it’s important to understand how computers work.
It may also surprise you to learn that computers themselves are rather simple machines. At the heart of a computer is a Central Processing Unit (CPU). This is essentially a math machine. It performs addition, subtraction, and other arithmetical operations on numbers. Everything you see when you operate your computer is all built upon a CPU crunching numbers many millions of times per second. Isn’t it amazing what can come from just numbers?
The CPU stores the numbers it acts upon in small memory units called registers. The CPU is able to read numbers into registers from the computer’s main memory, known as Random Access Memory (RAM). It’s also able to write the number stored in a register back into RAM. This allows the CPU to work with large amounts of data that wouldn’t all fit in the bank of registers.
Here is a diagram of how this works:

As the CPU pulls values from RAM into its registers, it uses those values in its math unit and stores the results back in another register.
Each time the CPU makes an addition, a subtraction, a read from RAM or a write to RAM, it’s executing a single instruction. Each computer program is usually made up of thousands to millions of instructions. A complex computer program such as your operating system, be it iOS, Android, macOS, Windows or Linux (yes, they’re computer programs too!), may have many millions of instructions in total.
It’s entirely possible to write individual instructions to tell a computer what to do, but for all but the simplest programs, it would be immensely time-consuming and tedious. This is because most computer programs aim to do much more than simple math — computer programs let you surf the internet, manipulate images, and allow you to chat with your friends.
Instead of writing individual instructions, you write code in a specific programming language, which in your case will be Kotlin. This code is put through a computer program called a compiler, which converts the code into instructions the CPU knows how to execute. Each line of code you write will turn into many instructions — some lines could end up being tens of instructions!
In the case of Kotlin, with its origins as a language on the Java Virtual Machine or JVM, there is an extra layer between the compiler and the OS. The Kotlin compiler creates what is known as bytecode, which gets run on the JVM and converted to native code along the way. Kotlin began on the JVM but now it is possible to compile Kotlin directly to native code, as you’ll see later in the book.
Representing numbers
As you know by now, numbers are a computer’s bread and butter, the fundamental basis of everything it does. Whatever information you send to the compiler will eventually become a number. For example, each character within a block of text is represented by a number. You’ll learn more about this in Chapter 3, “Types & Operations,” which delves into types including strings, the computer term for a block of text.
Images are no exception. In a computer, each image is also represented by a series of numbers. An image is split into many thousands, or even millions, of picture elements called pixels, where each pixel is a solid color. If you look closely at your computer screen, you may be able to make out these blocks. That is unless you have a particularly high-resolution display where the pixels are incredibly small! Each of these solid color pixels is usually represented by three numbers: one for the amount of red, one for the amount of green and one for the amount of blue. For example, an entirely red pixel would be 100% red, 0% green and 0% blue.
The numbers the CPU works with are notably different from those you are used to. When you deal with numbers in day-to-day life, you work with them in base 10, otherwise known as the decimal system. Having used this numerical system for so long, you intuitively understand how it works. So that you can you can appreciate the CPU’s point of view, consider how base 10 works.
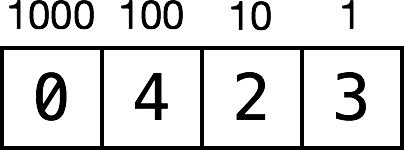
The decimal or base 10 number 423 contains three units, two tens and four hundreds:
In the base 10 system, each digit of a number can have a value of 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9, giving a total of 10 possible values for each digit. Yep, that’s why it’s called base 10!
But the true value of each digit depends on its position within the number. Moving from right to left, each digit gets multiplied by an increasing power of 10. So the multiplier for the far-right position is 10 to the power of 0, which is 1. Moving to the left, the next multiplier is 10 to the power of 1, which is 10. Moving again to the left, the next multiplier is 10 to the power of 2, which is 100. And so on.
This means each digit has a value ten times that of the digit to its right. The number 423 is equal to the following:
(0 * 1000) + (4 * 100) + (2 * 10) + (3 * 1) = 423
Binary numbers
Because you’ve been trained to operate in base 10, you don’t have to think about how to read most numbers — it feels quite natural. But to a computer, base 10 is way too complicated! Computers are simple-minded, remember? They like to work with base 2.
Base 2 is often called binary, which you’ve likely heard of before. It follows that base 2 has only two options for each digit: 0 or 1.
Almost all modern computers use binary because at the physical level, it’s easiest to handle only two options for each digit. In digital electronic circuitry, which is mostly what comprises a computer, the presence of an electrical voltage is 1 and the absence is 0 — that’s base 2!
Note: There have been computers both real and imagined that use the ternary numeral system, which has three possible values instead of two. Computer scientists, engineers and dedicated hackers continue to explore the possibilities of a base-3 computer. See https://en.wikipedia.org/wiki/Ternary_computer and http://hackaday.com/tag/ternary-computer/.
Here’s a representation of the base 2 number 1101:
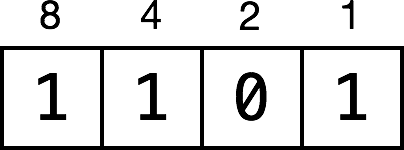
In the base 10 number system, the place values increase by a factor of 10: 1, 10, 100, 1000, etc. In base 2, they increase by a factor of 2: 1, 2, 4, 8, 16, etc. The general rule is to multiply each digit by an increasing power of the base number — in this case, powers of 2 — moving from right to left.
So the far-right digit represents (1 * 2⁰), equal to (1 * 1), which is 1. The next digit to the left represents (0 * 2¹), equal to (0 * 2), which is 0. In the illustration above, you can see the powers of 2 on top of the blocks.
Put another way, every power of 2 either is (1) or isn’t (0) present as a component of a binary number. The decimal version of a binary number is the sum of all the powers of 2 that make up that number. So the binary number 1101 is equal to:
(1 * 8) + (1 * 4) + (0 * 2) + (1 * 1) = 13
And if you wanted to convert the base 10 number 423 into binary, you would simply need to break down 423 into its component powers of 2. You would wind up with the following:
(1 * 256) + (1 * 128) + (0 * 64) + (1 * 32) + (0 * 16) + (0 * 8) + (1 * 4) + (1 * 2) + (1 * 1) = 423
As you can see by scanning the binary digits in the above equation, the resulting binary number is 110100111. You can prove to yourself that this is equal to 423 by doing the math! The computer term given to each digit of a binary number is a bit (a contraction of “binary digit”). Eight bits make up a byte. Four bits is called a nibble, a play on words that shows even old-school computer scientists had a sense of humor.
A computer’s limited memory means it can normally deal with numbers up to a certain length. Each register, for example, is usually 32 or 64 bits in length, which is why we speak of 32-bit and 64-bit CPUs.
Therefore, a 32-bit CPU can handle a maximum base-number of 4,294,967,295, which is the base 2 number 11111111111111111111111111111111. That is 32 ones—count them!
It’s possible for a computer to handle numbers that are larger than the CPU maximum, but the calculations have to be split up and managed in a special and longer way, much like the long multiplication you performed in school.
Hexadecimal numbers
As you can imagine, working with binary numbers can become quite tedious, because it can take a long time to write or type them. For this reason, in computer programming, we often use another number format known as hexadecimal, or hex for short. This is base 16.
Of course, there aren’t 16 distinct numbers to use for digits; there are only 10. To supplement these, we use the first six letters, a through f.
They are equivalent to decimal numbers like so:
-
a=10 -
b=11 -
c=12 -
d=13 -
e=14 -
f=15
Here’s a base 16 example using the same format as before:

Notice first that you can make hexadecimal numbers look like words. That means you can have a little bit of fun.
Now the values of each digit refer to powers of 16. In the same way as before, you can convert this number to decimal like so:
(12 * 4096) + (0 * 256) + (13 * 16) + (14 * 1) = 49374
You translate the letters to their decimal equivalents and then perform the usual calculations.
But why bother with this?
Hexadecimal is important because each hexadecimal digit can represent precisely four binary digits. The binary number 1111 is equivalent to hexadecimal f. It follows that you can simply concatenate the binary digits representing each hexadecimal digit, creating a hexadecimal number that is shorter than its binary or decimal equivalents.
For example, consider the number c0de from above:
c = 1100
0 = 0000
d = 1101
e = 1110
c0de = 1100 0000 1101 1110
This turns out to be rather helpful, given how computers use long 32-bit or 64-bit binary numbers. Recall that the longest 32-bit number in decimal is 4,294,967,295. In hexadecimal, it is ffffffff. That’s much more compact and clear.
How code works
Computers have a lot of constraints, and by themselves, they can only do a small number of things. The power that the computer programmer adds, through coding, is putting these small things together, in the right order, to produce something much bigger.
Coding is much like writing a recipe. You assemble ingredients (the data) and give the computer a step-by-step recipe for how to use them.
Here’s an example:
Step 1. Load photo from hard drive.
Step 2. Resize photo to 400 pixels wide by 300 pixels high.
Step 3. Apply sepia filter to photo.
Step 4. Print photo.
This is what’s known as pseudo-code. It isn’t written in a valid computer programming language, but it represents the algorithm that you want to use. In this case, the algorithm takes a photo, resizes it, applies a filter and then prints it. It’s a relatively straightforward algorithm, but it’s an algorithm nonetheless!
Kotlin code is just like this: a step-by-step list of instructions for the computer. These instructions will get more complex as you read through this book, but the principle is the same: You are simply telling the computer what to do, one step at a time.
Each programming language is a high-level, pre-defined way of expressing these steps. The compiler knows how to interpret the code you write and convert it into instructions that the CPU can execute.
There are many different programming languages, each with its own advantages and disadvantages. Kotlin is an extremely modern language. It incorporates the strengths of many other languages while ironing out some of their weaknesses. In years to come, programmers will look back on Kotlin as being old and crusty, too. But for now, it’s an extremely exciting language because it is quickly evolving.
This has been a brief tour of computer hardware, number representation and code, and how they all work together to create a modern program. That was a lot to cover in one section! Now it’s time to learn about the tools you’ll use to write in Kotlin as you follow along with this book.
Getting started with Kotlin
Now that you know how computers work, it’s time to start writing some Kotlin!
You may wish to follow along with your own IntelliJ IDEA project. Simply create one using the instructions from the first chapter and type in the code as you go.
First up is something that helps you organize your code. Read on!
Code comments
The Kotlin compiler generates bytecode or executable code from your source code. To accomplish this, it uses a detailed set of rules you will learn about in this book. Sometimes these details can obscure the big picture of why you wrote your code a certain way or even what problem you are solving. To prevent this, it’s good to document what you wrote so that the next human who passes by will be able to make sense of your work. That next human, after all, may be a future you.
Kotlin, like most other programming languages, allows you to document your code through the use of what are called comments. These allow you to write any text directly along side your code which is ignored by the compiler.
The first way to write a comment is like so:
// This is a comment. It is not executed.
This is a single line comment.
You could stack these up like so to allow you to write paragraphs:
// This is also a comment.
// Over multiple lines.
However, there is a better way to write comments which span multiple lines. Like so:
/* This is also a comment.
Over many..
many...
many lines. */
This is a multi-line comment. The start is denoted by /* and the end is denoted by */. Simple!
Kotlin also allows you to nest comments, like so:
/* This is a comment.
/* And inside it
is
another comment.
*/
Back to the first.
*/
This might not seem particularly interesting, but it may be if you have seen other programming languages. Many do not allow you to nest comments like this as when it sees the first */ it thinks you are closing the first comment. You should use code comments where necessary to document your code, explain your reasoning, or simply to leave jokes for your colleagues.
Printing out
It’s also useful to see the results of what your code is doing. In Kotlin, you can achieve this through the use of the println command.
println will output whatever you want to the console.
For example, consider the following code:
println("Hello, Kotlin Apprentice reader!")
This will output a nice message to the console, like so:
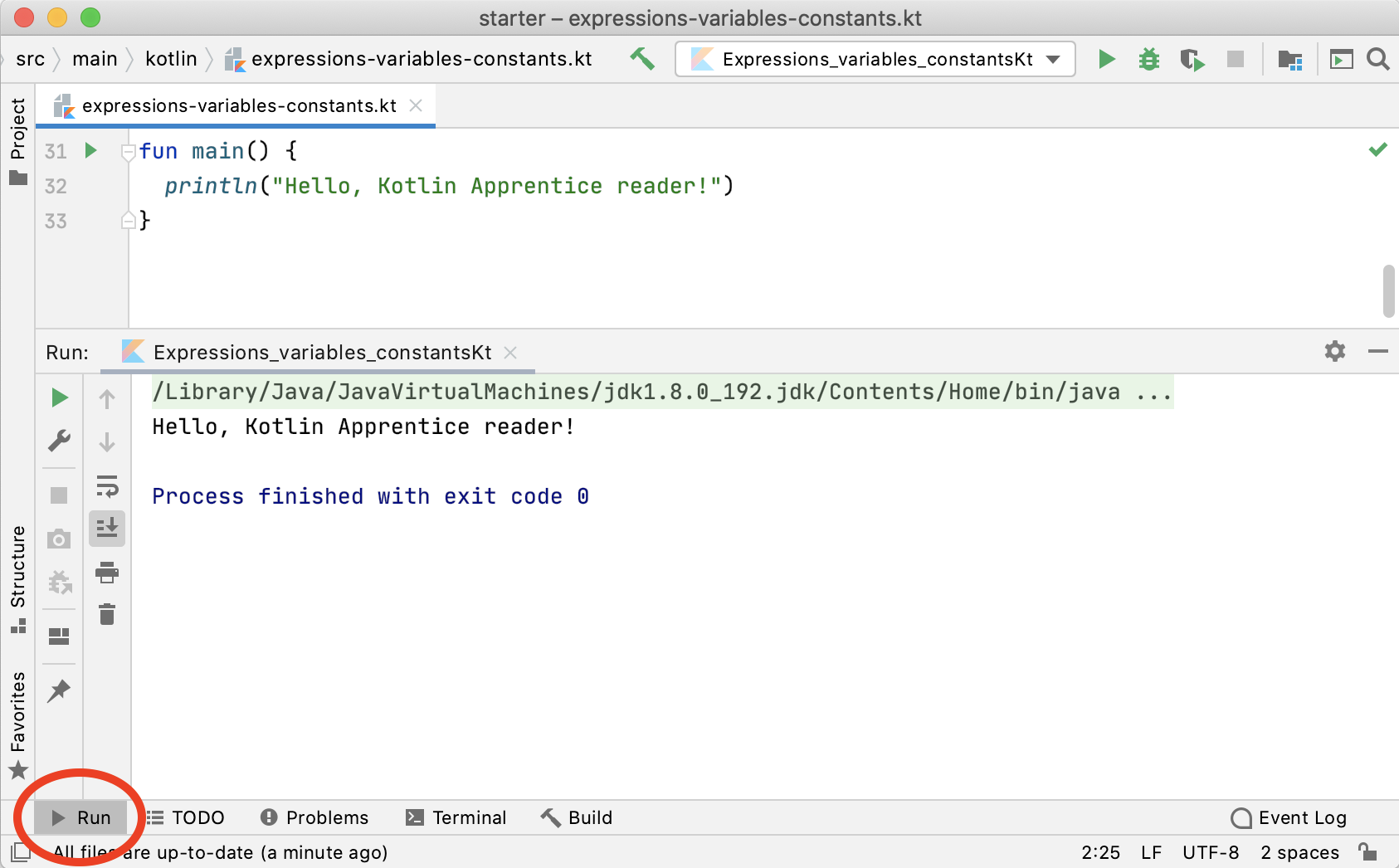
You can hide or show the console using the Run button at the bottom highlighted with the red oval in the picture above.
Arithmetic operations
When you take one or more pieces of data and turn them into another piece of data, this is known as an operation.
The simplest way to understand operations is to think about arithmetic. The addition operation takes two numbers and converts them into the sum of the two numbers. The subtraction operation takes two numbers and converts them into the difference of the two numbers. You’ll find simple arithmetic all over your apps; from tallying the number of “likes” on a post, to calculating the correct size and position of a button or a window, numbers are indeed everywhere!
In this section, you’ll learn about the various arithmetic operations that Kotlin has to offer by considering how they apply to numbers. In later chapters, you see operations for types other than numbers.
Simple operations
All operations in Kotlin use a symbol known as the operator to denote the type of operation they perform. Consider the four arithmetic operations you learned in your early school days: addition, subtraction, multiplication and division.
For these simple operations, Kotlin uses the following operators:
- Add:
+ - Subtract:
- - Multiply:
* - Divide:
/
These operators are used like so:
2 + 6
10 - 2
2 * 4
24 / 3
Each of these lines is what is known as an expression. An expression has a value. In these cases, all four expressions have the same value: 8. You write the code to perform these arithmetic operations much as you would write it if you were using pen and paper.
In your IDE, you can see the values of these expressions as output in the console using println():
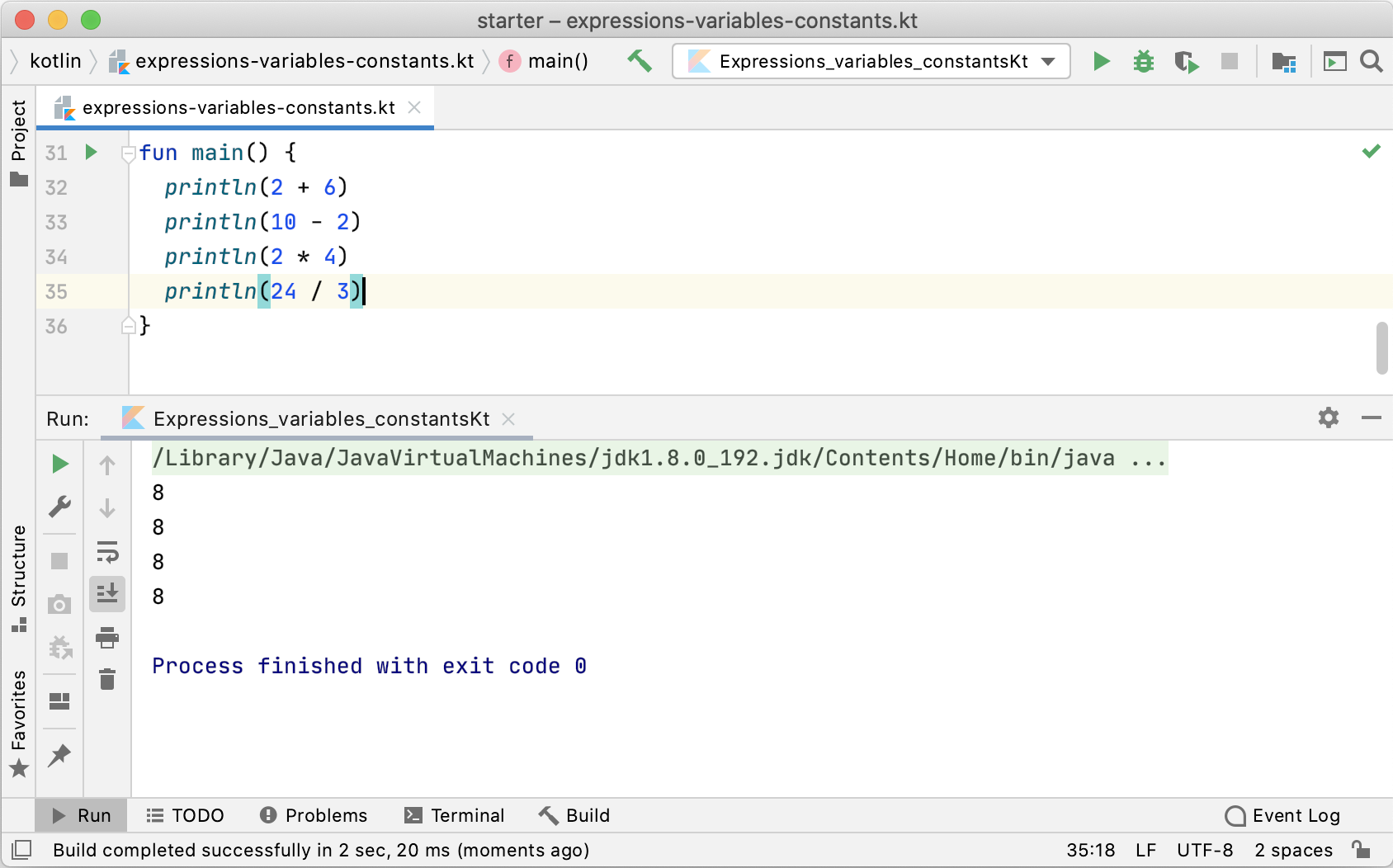
If you want, you can remove the whitespace surrounding the operator:
2+6
You can even mix where you put the whitespace. For example:
2+6 // OK
2 + 6 // OK
2 +6 // OK
2+ 6 // OK
It’s often easier to read expressions if you have white space on either side of the operator.
Decimal numbers
All of the operations above have used whole numbers, more formally known as integers. However, as you know, not every number is whole.
As an example, consider the following:
22 / 7
This, you may be surprised to know, results in the number 3. This is because if you only use integers in your expression, Kotlin makes the result an integer also. In this case, the result is rounded down to the next integer.
You can tell Kotlin to use decimal numbers by changing it to the following:
22.0 / 7.0
This time, the result is 3.142857142857143 as expected.
The remainder operation
The four operations you’ve seen so far are easy to understand because you’ve been doing them for most of your life. Kotlin also has more complex operations you can use, all of them standard mathematical operations, just less common ones. Let’s turn to them now.
The first of these is the remainder operation, also called the modulo operation. In division, the denominator goes into the numerator a whole number of times, plus a remainder. This remainder is exactly what the remainder operation gives. For example, 10 modulo 3 equals 1, because 3 goes into 10 three times, with a remainder of 1.
In Kotlin, the remainder operator is the % symbol, and you use it like so:
28 % 10
In this case, the result equals 8, because 10 goes into 28 twice with a remainder of 8. If you want to compute the same thing using decimal numbers you do it like so:
28.0 % 10.0
The result is identical to % when there are no decimals, which you can see by printing it out using a format specifier:
println("%.0f".format(28.0 % 10.0))
Shift operations
The Shift left and Shift right operations take the binary form of a decimal number and shift the digits left or right, respectively. Then they return the decimal form of the new binary number.
For example, the decimal number 14 in binary, padded to 8 digits, is 00001110. Shifting this left by two places results in 00111000, which is 56 in decimal.
Here’s an illustration of what happens during this shift operation:
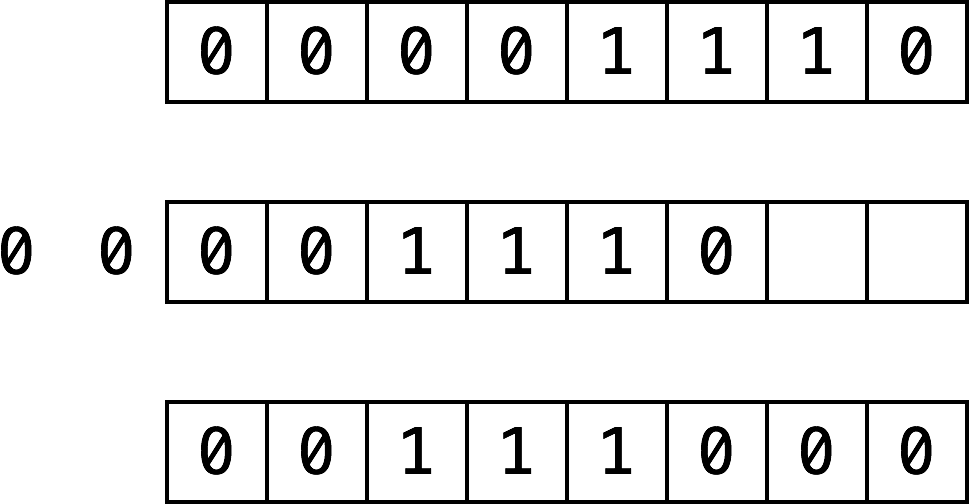
The digits that come in to fill the empty spots on the right become 0. The digits that fall off the end on the left are lost. Shifting right is the same, but the digits move to the right. The Kotlin functions for these two operations are as follows:
- Shift left:
shl - Shift right:
shr
These are infix functions that you place in between the operands so that the function call looks like an operation. You’ll learn more about infix functions later.
Here’s an example:
1 shl 3
32 shr 2
Both of these values equal the number 8.
One reason for using shifts is to make multiplying or dividing by powers of two easy. Notice that shifting left by one is the same as multiplying by two, shifting left by two is the same as multiplying by four, and so on. Likewise, shifting right by one is the same as dividing by two, shifting right by two is the same as dividing by four, and so on.
In the old days, code often made use of this trick because shifting bits is much simpler for a CPU to do than complex multiplication and division arithmetic. Therefore the code was quicker if it used shifting. However these days, CPUs are much faster and compilers can even convert multiplication and division by powers of two into shifts for you. So you’ll see shifting only for binary twiddling, which you probably won’t see unless you become an embedded systems programmer!
Order of operations
Of course, it’s likely that when you calculate a value, you’ll want to use multiple operators. Here’s an example of how to do this in Kotlin:
((8000 / (5 * 10)) - 32) shr (29 % 5)
Note the use of parentheses, which in Kotlin serve two purposes: to make it clear to anyone reading the code — including yourself — what you meant, and to disambiguate.
For example, consider the following:
350 / 5 + 2
Does this equal 72 (350 divided by 5, plus 2) or 50 (350 divided by 7)? Those of you who paid attention in school will be screaming “72!” And you would be right!
Kotlin uses the same reasoning and achieves this through what’s known as operator precedence. The division operator (/) has a higher precedence than the addition operator (+), so in this example, the code executes the division operation first.
If you wanted Kotlin to do the addition first — that is, to return 50 — then you could use parentheses like so:
350 / (5 + 2)
The precedence rules follow the same that you learned in math at school. Multiply and divide have the same precedence, higher than add and subtract which also have the same precedence.
Math functions
Kotlin also has a vast range of math functions in it’s standard library for you to use when necessary. You never know when you need to pull out some trigonometry, especially when you’re a pro at Kotlin and writing those complex games!
To use the following math functions, make sure you have this import near the top of your file. Otherwise, IntelliJ IDEA will tell you it can’t find these functions.
import kotlin.math.*
For example, consider the following:
sin(45 * PI / 180)
// 0.7071067811865475
cos(135 * PI / 180)
// -0.7071067811865475
These compute the sine and cosine respectively. Notice how both make use of PI which is a constant Kotlin provides us, ready-made with 𝜋 to as much precision as is possible by the computer.
Then there’s this:
sqrt(2.0)
// 1.414213562373095
This computes the square root of 2. Did you know that sin(45°) equals 1 over the square root of 2?
Not to mention these would be a shame:
max(5, 10)
// 10
min(-5, -10)
// -10
These compute the maximum and minimum of two numbers respectively.
If you’re particularly adventurous you can even combine these functions like so:
max(sqrt(2.0), PI / 2)
// 1.570796326794897
Naming data
At its simplest, computer programming is all about manipulating data. Remember, everything you see on your screen can be reduced to numbers that you send to the CPU. Sometimes you yourself represent and work with this data as various types of numbers, but other times the data comes in more complex forms such as text, images and collections.
In your Kotlin code, you can give each piece of data a name you can use to refer to it later. The name carries with it an associated type that denotes what sort of data the name refers to, such as text, numbers, or a date.
You’ll learn about some of the basic types in this chapter, and you’ll encounter many other types throughout the rest of this book.
Constants
Take a look at this:
val number: Int = 10
This uses the val keyword to declare a constant called number which is of type Int. Then it sets the value of the constant to the number 10.
Note: Thinking back to operators, here’s another one. The equals sign,
=, is known as the assignment operator.
The type Int can store integers. The way you store decimal numbers is like so:
val pi: Double = 3.14159
This is similar to the Int constant, except the name and the type are different. This time, the constant is a Double, a type that can store decimals with high precision.
There’s also a type called Float, short for floating point, that stores decimals with lower precision than Double. In fact, Double has about double the precision of Float, which is why it’s called Double in the first place. A Float takes up less memory than a Double but generally, memory use for numbers isn’t a huge issue and you’ll see Double used in most places.
Even though we call an item created with val a “constant,” it’s more correct to say that the identifier marked with val is what is constant.
Once you’ve declared a constant, you can’t change its data. For example, consider the following code:
val number: Int = 10
number = 0
This code produces an error:
Val cannot be reassigned
In your IDE, you would see the error represented this way:
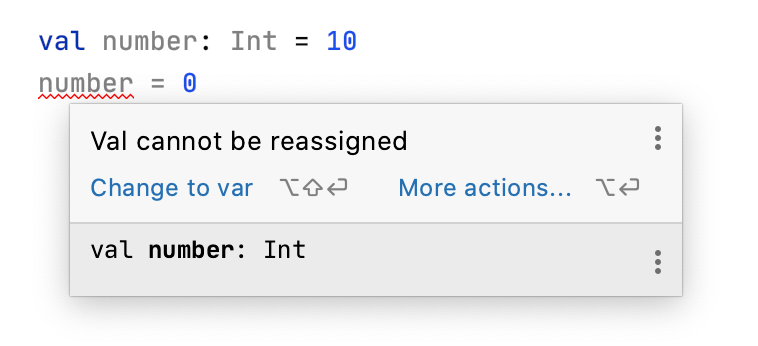
Constants are useful for values that aren’t going to change. For example, if you were modeling an airplane and needed to keep track of the total number of seats available, you could use a constant.
You might even use a constant for something like a person’s age. Even though their age will change as their birthday comes, you might only be concerned with their age at this particular instant.
In certain situations, for example, at the top level of your code outside of any functions, you can add the const keyword to a val to mark it as a compile-time constant:
const val reallyConstant: Int = 42
Values marked with const must initialized with a String or a primitive type such as an Int or Double. You can also use const inside a Kotlin type that you’ll learn about in Chapter 12: “Objects.”
Variables
Often you want to change the data behind a name. For example, if you were keeping track of your bank account balance with deposits and withdrawals, you might use a variable rather than a constant.
If your program’s data never changed, then it would be a rather boring program! But as you’ve seen, it’s not possible to change the data behind a constant.
When you know you’ll need to change some data, you should use a variable to represent that data instead of a constant. You declare a variable in a similar way, like so:
var variableNumber: Int = 42
Only the first part of the statement is different: You declare constants using val, whereas you declare variables using var.
Once you’ve declared a variable, you’re free to change it to whatever you wish, as long as the type remains the same. For example, to change the variable declared above, you could do this:
variableNumber = 0
variableNumber = 1_000_000
To change a variable, you simply assign it a new value.
Note: In Kotlin, you can optionally use underscores to make larger numbers more human-readable. The quantity and placement of the underscores is up to you.
Using meaningful names
Always try to choose meaningful names for your variables and constants. Good names can act as documentation and make your code easy to read. A good name specifically describes the role of variable or constant. Here are some examples of good names:
personAgenumberOfPeoplegradePointAverage
Often a bad name is simply not descriptive enough. Here are some examples of bad names:
atempaverage
The key is to ensure that you’ll understand what the variable or constant refers to when you read it again later. Don’t make the mistake of thinking you have an infallible memory! It’s common in computer programming to look back at your own code as early as a day or two later and have forgotten what it does. Make it easier for yourself by giving your variables and constants intuitive, precise names.
Also, note how the names above are written. In Kotlin, it is common to camel case names. For variables and constants, follow these rules to properly case your names:
- Start with a lowercase letter.
- If the name is made up of multiple words, join them together and start every word other than the first word with an uppercase letter.
- If one of these words is an abbreviation, follow the same pattern as if it was a word (e.g.,
sourceUrlandurlDescription).
Increment and decrement
A common operation that you will need is to be able to increment or decrement a variable. In Kotlin, this is achieved like so:
var counter: Int = 0
counter += 1
// counter = 1
counter -= 1
// counter = 0
The counter variable begins as 0. The increment sets its value to 1, and then the decrement sets its value back to 0.
These operators are similar to the assignment operator (=), except they also perform an addition or subtraction. They take the current value of the variable, add or subtract the given value and assign the result to the variable.
In other words, the code above is shorthand for the following:
var counter: Int = 0
counter = counter + 1
counter = counter - 1
Similarly, the *= and /= operators do the equivalent for multiplication and division, respectively:
counter = 10
counter *= 3 // same as counter = counter * 3
// counter = 30
counter /= 2 // same as counter = counter / 2
// counter = 15
Mini-exercises
If you haven’t been following along with the code in IntelliJ IDEA, now’s the time to try some exercises to test yourself!
- Declare a constant of type
IntcalledmyAgeand set it to your age. - Declare a variable of type
DoublecalledaverageAge. Initially, set it to your own age. Then, set it to the average of your age and the age of30. - Create a constant called
testNumberand initialize it with whatever integer you’d like. Next, create another constant calledevenOddand set it equal totestNumbermodulo 2. Now changetestNumberto various numbers. What do you notice aboutevenOdd? - Create a variable called
answerand initialize it with the value0. Increment it by1. Add10to it. Multiply it by10. Then, shift it to the right by3. After all of these operations, what’s the answer?
Challenges
Before moving on, here are some challenges to test your knowledge of variables and constants. You can try the code in IntelliJ IDEA to check your answers. If you get stuck, check out the solutions included in the materials for this chapter.
-
Declare a constant
exerciseswith value 9 and a variableexercisesSolvedwith value 0. Increment this variable every time you solve an exercise (including this one). -
Given the following code:
age = 16
print(age)
age = 30
print(age)
Declare age so that it compiles. Did you use var or val?
- Consider the following code:
val a: Int = 46
val b: Int = 10
Work out what answer equals when you add the following lines of code:
// 1
val answer1: Int = (a * 100) + b
// 2
val answer2: Int = (a * 100) + (b * 100)
// 3
val answer3: Int = (a * 100) + (b / 10)
- Add parentheses to the following calculation. The parentheses should show the order in which the operations are performed and should not alter the result of the calculation.
5 * 3 - 4 / 2 * 2
-
Declare two constants
aandbof typeDoubleand assign both a value. Calculate the average ofaandband store the result in a constant namedaverage. -
A temperature expressed in °C can be converted to °F by multiplying by 1.8 then incrementing by 32. In this challenge, do the reverse: convert a temperature from °F to °C. Declare a constant named
fahrenheitof typeDoubleand assign it a value. Calculate the corresponding temperature in °C and store the result in a constant namedcelcius. -
Suppose the squares on a chessboard are numbered left to right, top to bottom, with 0 being the top-left square and 63 being the bottom-right square. Rows are numbered top to bottom, 0 to 7. Columns are numbered left to right, 0 to 7. Declare a constant
positionand assign it a value between 0 and 63. Calculate the corresponding row and column numbers and store the results in constants namedrowandcolumn. -
A circle is made up of 2𝜋 radians, corresponding with 360 degrees. Declare a constant
degreesof typeDoubleand assign it an initial value. Calculate the corresponding angle in radians and store the result in a constant namedradians. -
Declare four constants named
x1,y1,x2andy2of typeDouble. These constants represent the two-dimensional coordinates of two points. Calculate the distance between these two points and store the result in a constant nameddistance.
Key points
- Computers, at their most fundamental level, perform simple mathematics.
- A programming language allows you to write code, which the compiler converts into instructions that the CPU can execute. Kotlin code on the JVM is first converted to bytecode.
- Computers operate on numbers in base 2 form, otherwise known as binary.
- Code comments are denoted by a line starting with
//or multiple lines bookended with/*and*/. - Code comments can be used to document your code.
- You can use
printlnto write things to the console area. - The arithmetic operators are:
Add: +
Subtract: -
Multiply: *
Divide: /
Remainder: %
- Constants and variables give names to data.
- Once you’ve declared a constant, you can’t change its data, but you can change a variable’s data at any time.
- Always give variables and constants meaningful names to save yourself and your colleagues headaches later.
- Operators to perform arithmetic and then assign back to the variable:
Add and assign: +=
Subtract and assign: -=
Multiply and assign: *=
Divide and assign: /=
Where to go from here?
In this chapter, you’ve dealt with only numbers, both integers and decimals. Of course, there’s more to the world of code than that! In the next chapter, you’re going to learn about more types such as strings, which allow you to store text.