Introduction to A* Pathfinding
This is a blog post by iOS Tutorial Team member Johann Fradj, a software developer currently full-time dedicated to iOS. He is the co-founder of Hot Apps Factory which is the creator of App Cooker. Have you ever had a game where you wanted to make monsters or players move to a particular point, while […] By Ray Wenderlich.
Sign up/Sign in
With a free Kodeco account you can download source code, track your progress, bookmark, personalise your learner profile and more!
Create accountAlready a member of Kodeco? Sign in
Sign up/Sign in
With a free Kodeco account you can download source code, track your progress, bookmark, personalise your learner profile and more!
Create accountAlready a member of Kodeco? Sign in
Contents
Introduction to A* Pathfinding
20 mins
More About H
Recall that H is the estimated movement cost (in number of squares for this game) from the current square to the destination point.
The closer the estimated movement cost is to the actual cost, the more accurate the final path will be. If the estimate is off, it is possible the path generated will not be the shortest (but it will probably be close). This topic is quite complex so will not be covered in this tutorial series, but I have provided a link explaining it very well at the end of the article.
To put it simply, we will use the “Manhattan distance method” (Also called “Manhattan length” or “city block distance”) that just counts the number of horizontal and vertical square remaining to reach point B without taking into account of any obstacles or differences of land.
For example, here’s a diagram that shows using the “city block distance” to estimate H (shown in black) from various starts and destinations:
The A* Algorithm
So now that you know how to compute the score of each square (we’ll call this F, which again is equal to G + H), let’s see how the A* algorithm works.
The cat will find the shortest path by repeating the following steps:
- Get the square on the open list which has the lowest score. Let’s call this square S.
- Remove S from the open list and add S to the closed list.
- For each square T in S’s walkable adjacent tiles:
- If T is in the closed list: Ignore it.
- If T is not in the open list: Add it and compute its score.
- If T is already in the open list: Check if the F score is lower when we use the current generated path to get there. If it is, update its score and update its parent as well.
- If T is in the closed list: Ignore it.
- If T is not in the open list: Add it and compute its score.
- If T is already in the open list: Check if the F score is lower when we use the current generated path to get there. If it is, update its score and update its parent as well.
Don’t worry if you’re still a bit confused about how this works – we’ll walk through an example so you can see it working step by step! :]
The Cat’s Path
Let’s go through the example of our lazy cat on the way to a bone.
In the diagrams below, I’ve listed the values for F = G + H according to the following:
- F (score for square): Top left corner
- G (cost from A to square): Bottom left corner
- H (estimated cost from square to B): Bottom right corner
Also, the arrow shows the movement direction to get to that square.
Finally, on each step the red squares indicate the closed list and the green squares indicate the open list.
OK, so let’s begin!
Step 1
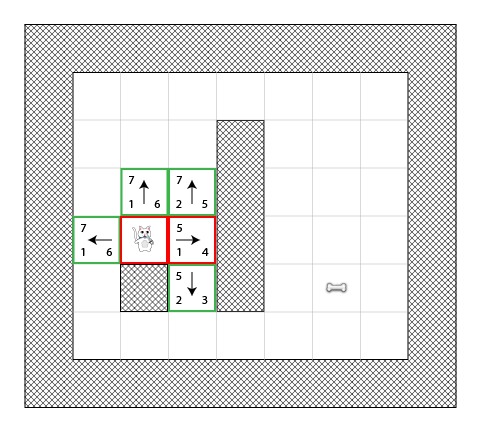
In the first step, the cat determines the walkable adjacent squares to its start position (point A), computes their F scores, and adds them to its open list:
You can see that the H value is listed for each square (two have 6 and one has 4). I recommend counting out the squares according to the “city block distance” to make sure you understand how that part works.
Also note that the F value (in the upper right) is just the sum of G+H (lower left and lower right).
Step 2
In the next step, the cat chooses the square with the lowest F score, adds it to the closed list, and retrieves its adjacent squares.
So you’ll see here that the square with the lowest cost was the one that had F as 4. It tried to add any tile adjacent to this to open list (and calculate their score), except notice that it couldn’t add the cat tile (because it was already on the closed list) or the wall tile (because it wasn’t walkable).
Notice for the two new tiles added to the open list, the G values are increased by one because they are 2 tiles away from the starting point. You might also like to count out the “city block distance” to make sure you understand the H values for each of the new tiles.
Step 3
Again, we choose the tile with the lowest F score (5) and continue to iterate:
In this case, there was only one possible tile to add to the open list, because one was already on the closed list and two were walls.
Step 4
Now we have an interesting case. As you can see in the previous screenshot, there are 4 squares with the same F score as 7 – what do we do?!
There are various solutions we could use, but one simple (and fast) way is to keep following the tile most recently added to the open list. So continuing on with the most recent square we have:
This time two tiles were adjacent and walkable, and we calculate their scores as usual.
Step 5
Again we choose the tile with the lowest score (7) and in case of a tie choose the most recent:
Just one possibility added this time. We’re getting close!
Step 6
You get the drill by now! I bet you can guess the next step looks like the following:
We’re almost there, but this time you can see that there are actually two shortest paths to the bone we could choose between:
In our example there is 2 differents shortest paths:
- 1-2-3-4-5-6
- 1-2-3-4-5-7
It doesn’t really matter which of these we choose, it comes down to the actual implementation in code.
Step 7
Let’s iterate one more time from one of these squares:
Aha, the bone is in the open list!
Step 8
In the case where the target square is in the open list, the algorithm adds it to the closed list:
Then all the algorithm has to do is go backwards to figure out the final path!